Я не собираюсь оспаривать правила и сложившиеся традиции в альпинистской и туристической среде. Если положено переправу делать из сдвоенной основной веревки — значит надо делать так. Соблюдать правила или нет — личное дело каждого (кроме командира группы, ответственного за всех остальных, конечно же). Я выкладываю лишь результаты математических расчетов, которые могут быть интересны любознательным людям.
Условия задачи
Провисание груза на переправе обусловлено растяжением веревки. Предположим, что веревка растягивается не очень сильно, и её удлинение под нагрузкой подчиняется закону Гука.
Ослаблением натяжения веревки за счет затягивания узлов, упругости точек крепления переправы и подобными факторами мы пренебрежем.
Очевидно, что сильнее всего веревка натянута при расположении груза в середине переправы. Ради простоты расчетов мы будем рассматривать только такой случай.
Теория
Рассмотрим силы, действующие на груз, который подвешен в середине переправы. Нас интересует только вертикальная составляющая.
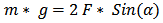
где m*g — сила тяжести, действующая на груз,
F — сила натяжения веревки,
α — угол отклонения веревки от горизонтали.
Сила натяжения веревки, согласно закону Гука, будет подчиняться следующей формуле:
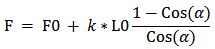
где F0 — сила предварительного натяжения веревки (без груза),
k — коэффициент жесткости веревки,
L0 — длина переправы.
Данных о коэффициенте жесткости альпинистских веревок мне найти не удалось. Пришлось провести эксперимент и порастягивать веревку безменом. Новая 8 мм статика дала значение порядка 2800 Н/м. Точность измерений оставляет желать лучшего, но порядок значений именно такой.
Подставим выражение для силы натяжения в первую формулу, получим следующее:
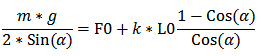
Получившееся уравнение даже имеет аналитическое решение в области действительных чиссел! :)
Нас интересует действительное положительное решение относительно α в окресностях ноля. Я не буду его приводить в аналитическом виде, оно слишком громоздко. Вычислив α, легко получить и все остальные нужные нам параметры.
Расчеты
Входные данные: масса груза, длина переправы, преднатяжение веревки. Нас интересуют натяжение веревки под грузом, максимальное провисание переправы и коэффициент запаса прочности.
Рассмотрим наиболее типичный случай. Переправляем груз массой 80 кг через реку шириной 30 м. Веревка основная, сдвоенная. Гарантированное усилие на разрыв — 44 кН. Жесткость веревки примем за 6000 Н/м (=2*3000 Н/м, т.к. веревка сдвоенная). Поскольку в переправе из сдвоенной веревки каждая из веревок натягивается независимо, то усилие преднатяга также можно сделать вдвое большим, пусть это будет 3000 Н (=2*1500 Н).
| Масса груза | 80 кг | Максимальное усилие на разрыв | 44000 Н |
| Длина переправы | 30 м | Натяжение веревки под грузом | 3911 Н |
| Преднатяжение веревки | 3000 Н | Максимальное провисание груза | 3.02 м |
| Коэффициент жесткости веревки | 6000 Н/м | Коэффициент запаса прочности | 11.25 |
Что касается провиса переправы, вполне ожидаемый и согласующийся с практикой результат. Даже при условии очень сильного натяжения переправы точки крепления следует располагать повыше над водой. Посмотрим теперь, что будет, если использовать одинарную веревку?
| Масса груза | 80 кг | Максимальное усилие на разрыв | 22000 Н |
| Длина переправы | 30 м | Натяжение веревки под грузом | 2568 Н |
| Преднатяжение веревки | 1500 Н | Максимальное провисание груза | 4.63 м |
| Коэффициент жесткости веревки | 3000 Н/м | Коэффициент запаса прочности | 8.56 |
Удивительно, но коэффициент запаса прочности изменился не так уж и сильно! Я нахожу объяснение этому в том, что веревка сильнее растягивается.
Выходит, что больший практический смысл использовать двойную веревку в переправе отнюдь не в повышенной надежности, а уменьшении провиса! С надежностью даже в этом случае всё очень-очень хорошо. Считаю, что даже трех- четырехкратного запаса вполне бы хватило, даже учитывая снижение прочности за счет узлов и за счет старения веревки.
Возьмем вариант с одинарной основной веревкой за некий эталон и попробуем изменять другие параметры. Начнем с массы.
| Масса груза | 50 кг | Максимальное усилие на разрыв | 22000 Н |
| Длина переправы | 30 м | Натяжение веревки под грузом | 2112 Н |
| Преднатяжение веревки | 1500 Н | Максимальное провисание груза | 3.50 м |
| Коэффициент жесткости веревки | 3000 Н/м | Коэффициент запаса прочности | 10.4 |
Уменьшение массы груза в полтора раза разительно снижает провисание переправы.
А что если сократить ширину реки, скажем, до 10 метров?
| Масса груза | 80 кг | Максимальное усилие на разрыв | 22000 Н |
| Длина переправы | 10 м | Натяжение веревки под грузом | 2059 Н |
| Преднатяжение веревки | 1500 Н | Максимальное провисание груза | 1.94 м |
| Коэффициент жесткости веревки | 3000 Н/м | Коэффициент запаса прочности | 10.68 |
Снова радикальное снижение провисания. Отсюда вывод: если деревья по берегам реки не позволяют закрепить переправу повыше, то есть большой резон искать место, где река сужается!
Наконец, рассмотрим самый жесткий случай: переправляем груз массой 100 кг по переправе длиной 50 м по одинарной веревке, умудрившись натянуть её до состояния струны в 5000 Н.
| Масса груза | 100 кг | Максимальное усилие на разрыв | 22000 Н |
| Длина переправы | 50 м | Натяжение веревки под грузом | 5581 Н |
| Преднатяжение веревки | 5000 Н | Максимальное провисание груза | 4.40 м |
| Коэффициент жесткости веревки | 3000 Н/м | Коэффициент запаса прочности | 3.94 |
Даже в этом случае коэффициент запаса прочности достаточен для безопасной переправы.
Рассмотрим еще один экстремальный случай. Вместо основной веревки возьмем одинарный 6 мм шнур.
| Масса груза | 80 кг | Максимальное усилие на разрыв | 7200 Н |
| Длина переправы | 30 м | Натяжение веревки под грузом | 2568 Н |
| Преднатяжение веревки | 1500 Н | Максимальное провисание груза | 4.63 м |
| Коэффициент жесткости веревки | 3000 Н/м | Коэффициент запаса прочности | 2.80 |
Разница с эталонным вариантом — только в максимальном усилии на разрыв веревки, которое в данном случае равно 7200 Н. Коэффициент жесткости примерно такой же (может чуть поменьше будет, но это не дает большого эффекта). Соответственно провис переправы тоже тот же самый. Разница — в коэффициенте запаса прочности, который оказывается равен 2.80. Чисто теоретически должно выдержать. Чисто практически я бы попробовал этот вариант только в самом крайнем, исключительном случае.
Выводы
Использование сдвоенной веревки осмыслено скорее с точки зрения уменьшения провиса переправы. На безопасность сдвоенная веревка влияет только лишь с той позиции, что если одна из веревок порвется, это не приведет к жертвам. Влияние на коэффициент запаса прочности за счет сдваивания минимально. И уж точно коэффициент не отличается в 2 раза, как это могло бы показаться на первый взгляд.
Провис переправы сильно зависит от массы груза.
Длина переправы влияет в основном на провис, а не на максимальное натяжение веревки, хотя определенная зависимость, конечно же, есть. При возможности следует делать переправу как можно короче.